

When using a diffraction grating to examine spectra and measure wavelength only the principal maximum with n=1 is used. By proportion, sin( θ) will also be small. Now consider the case when wavelength λ is small (eg blue light). We can see that when wavelength λ is large(eg red light) sin( θ) is large, because λ and sin( θ) are directly proportional to each other. If we rearrange our diffraction grating equation to make wavelength the subject, making n=1 for the first principal maxima to the right or left. However, for diffraction gratings the deviation of coloured rays is the reverse. It must be noted that the distribution of light intensity across a diffraction display remains that of a single slit.įrom intermediate physics you may remember 'red rays refract least', illustrated by the prism diagram below. So discrete bright fringes(principal maxima) are produced at specific angles for particular wavelengths of light. Using simple trigonometry, if d is the distance between slits, then the path difference is dsin( θ). The path difference between successive light rays must therefore be a whole number ( n) of wavelengths ( λ). Whenever this happens a bright fringe called a principal maxima is produced. So light rays diffracted at the same angle ( θ) and in phase with each other will interfere constructively. The clear spaces on a diffraction grating act as equally spaced slits. alter the relative intensities of principal maxima alter the angular positions of the principal maximaĢ. the absolute intensity of maxima increasesįor a particular value of N, the effect of altering the sum a+b is to:ġ. the angular position of maxima remains the sameĤ. the sharpness of the principal maxima increasesģ. as the intensities of the principal maxima increase the intensities of the subsidiary maxima decreaseĢ. The diffraction patterns below are obtained by varying N.ġ. of clear slits drawn on an opague glass slide a - the width of a clear area b - the width of an opague area d - width of a clear and an opague area L - length of glass slide Rearranging our single slit equation, with n=1 for the first minimum,Īs a result of the ratio λ/a being very small, sin( θ) ≈ θ in value. In practice the slit width ( a) is much larger than the wavelength ( λ) of light used.

Unfortunately lack of space precludes the derivation of further minima.Īs a general rule, the angular positions θ of the minima are given by: Using simple trigonometry, the path difference ( in red) is equal to a/2 sin( θ). So, for the first minimum, we look at the first and last waves in this segment(a/2) with a phase difference of λ/2 (π - pi radians). For each pair of light waves the phase difference is half a wave length and the vertical distance between wave points is a/2. The first light wave (1) in the upper half of the slit interferes destructively with the light wave (k) from the middle of the slit.Īnd so on, until light wave k+1 interferes with light wave 2k. The dark fringes(minima) are where pairs of light waves are in anti-phase and cancel out.Ĭonsider pairs of light waves interfering with each other across the width of the slit.

To frame an equation that predicts outcomes from this waveform, we must re-visit work on the superposition of waves.
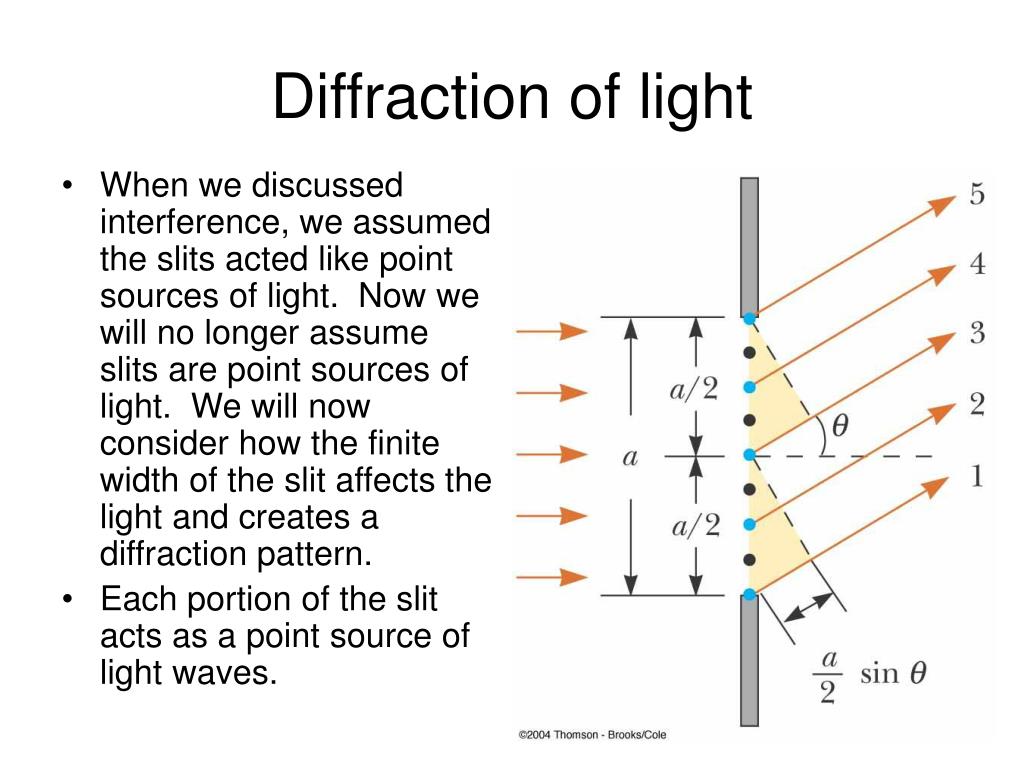
The secondary maxima are considerably dimmer than the central maximum(4.7% of the brightness). The diagram and image give a false impression regarding the relative brightness of fringes. Note that the central maximum is twice the width of other maxima and that all these have the same width. The diffraction pattern is graphed in terms of intensity and angle of deviation from the central position. Diffraction is the bending of light at an edge as a result of the superposition of wavelets from a plane wavefront.


 0 kommentar(er)
0 kommentar(er)
